Everything you need to know about Merkle trees

A Merkle tree or hash tree, named after the scientist Ralph Merkle, is a hash-based data formation that is used in cryptography and computer science.

Hash functions are used to make content uniform in length, to make it secure and for the identification of transactions in the blockchain. 

What is a Merkle tree?

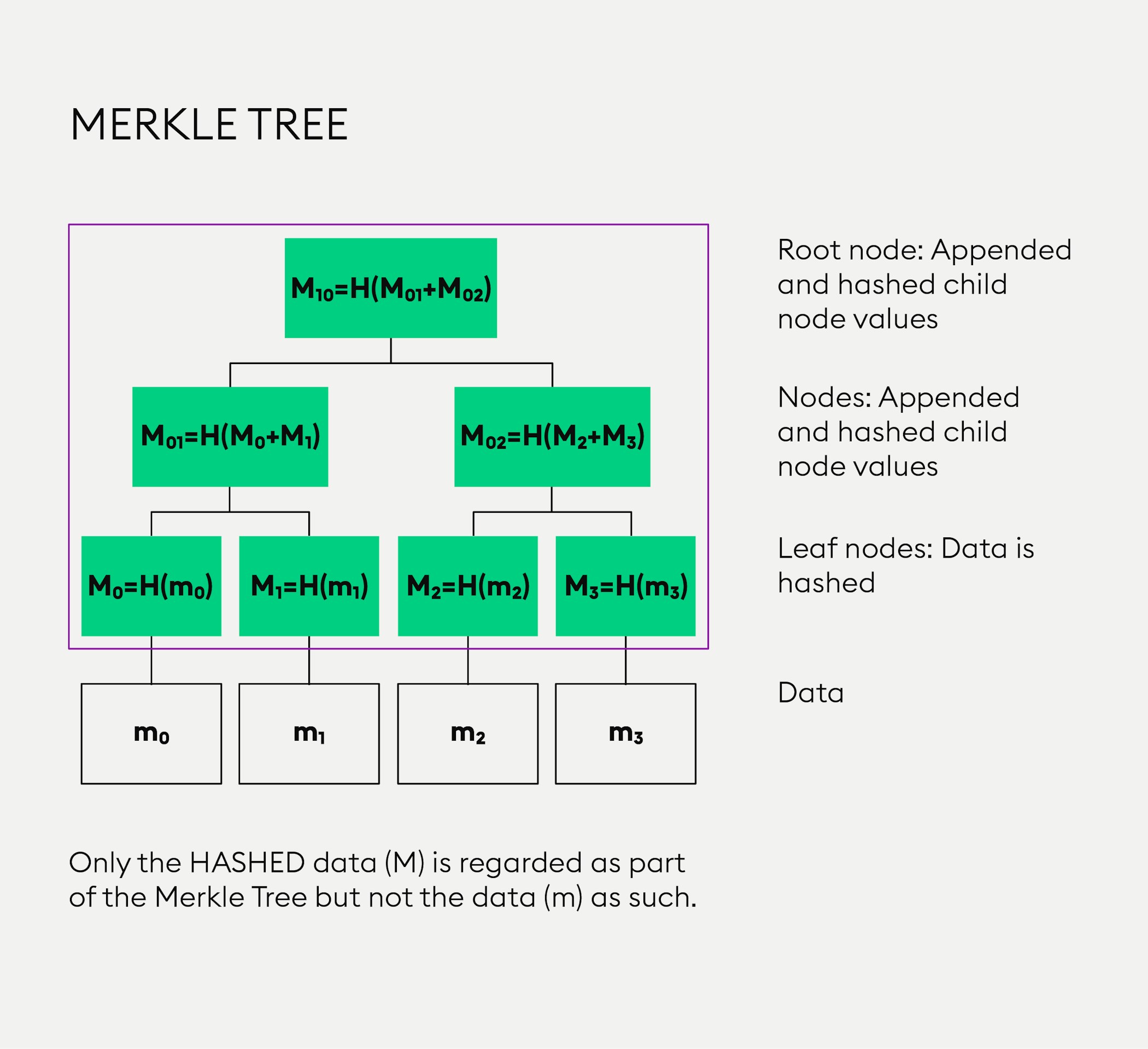
In the Bitcoin network, Merkle trees are used for data verification, which is efficient because hashes are used instead of a complete information file. A Merkle tree is a tree of hashed values as illustrated in the image below:

The blue boxes at the bottom - “m0”, “m1”, “m2” and “m3” - represent data. This data “m” is not considered a part of the Merkle tree. Now, if the value in such a box - with a lower-case letter “m” - is hashed, you receive a hashed value, indicated in the yellow box above with a capital letter “M”. 

Root node and leaf nodes

The yellow boxes in the infographic represent “leaf nodes” and indicate data that has been hashed. The two values “M0” and “M1” are appended, as indicated by a “+” sign and hashed together, as represented in the dark-grey box above, the result is another hashed value containing the “child node values”. Finally, these values are appended and hashed, resulting in a single “root”, also called the “Merkle root”. 

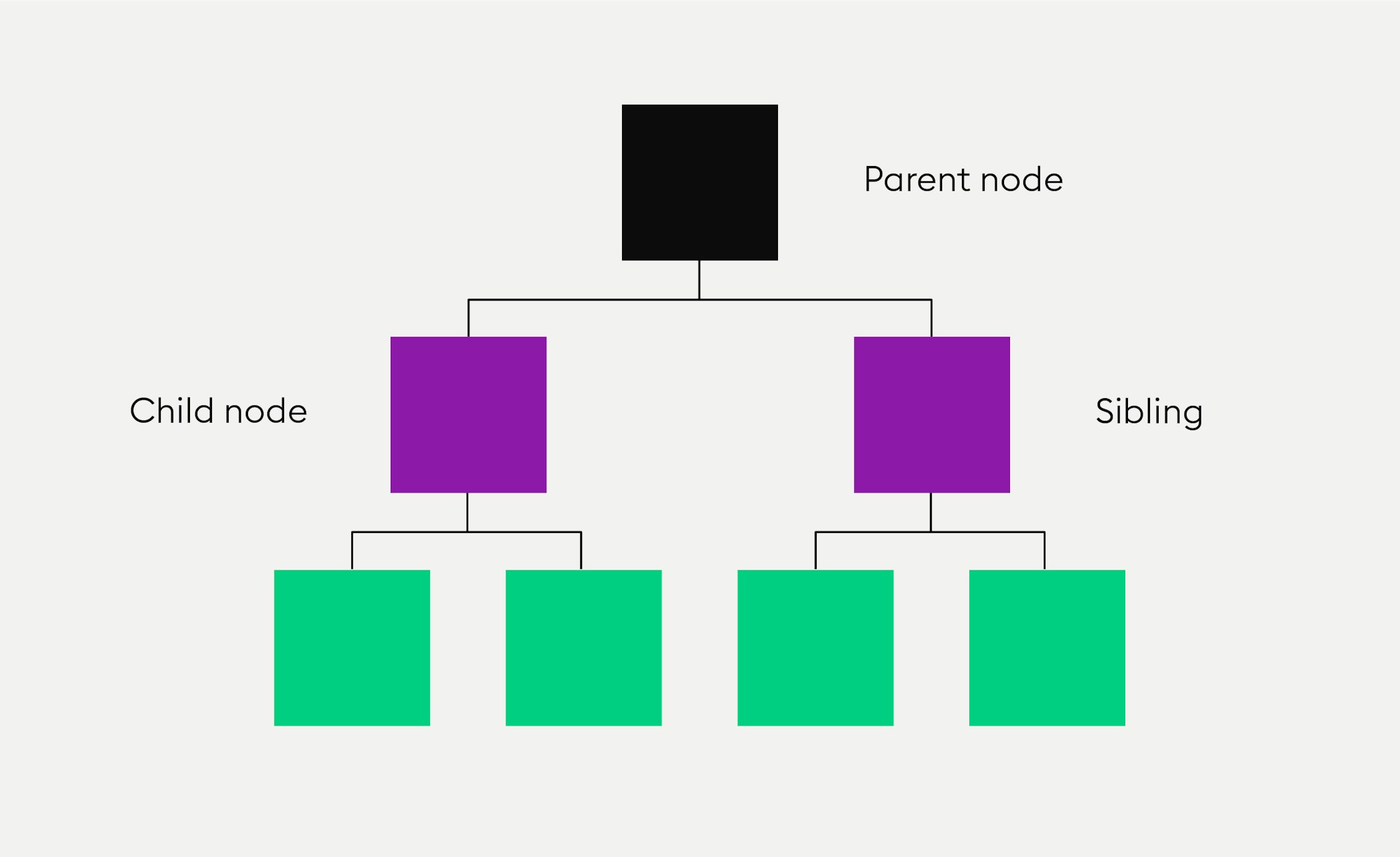
The two nodes beneath a parent node are the “child nodes” of that parent node. 

The root hash is the upper-most hash in the hash-based data structure. What is important to us, is the relation to Bitcoin, where this root is part of the block header. It ensures which transactions are present.

A Merkle tree uses a special type of descriptive terminology to describe the relationship among nodes and levels of nodes, such as used during the process of Simplified Payment Verification (SPV).

A node containing the values of the two nodes beneath it is the “parent” of those two nodes. If every node has, at most, two “child nodes” or “children”, this is called a binary hash tree. 

The two nodes beneath a parent node are the “child nodes” of this parent node. A child node next to another child node is the “sibling” of that child node. All nodes on the bottom that don’t have any “children” are called “leaf nodes”, they are on the same level.

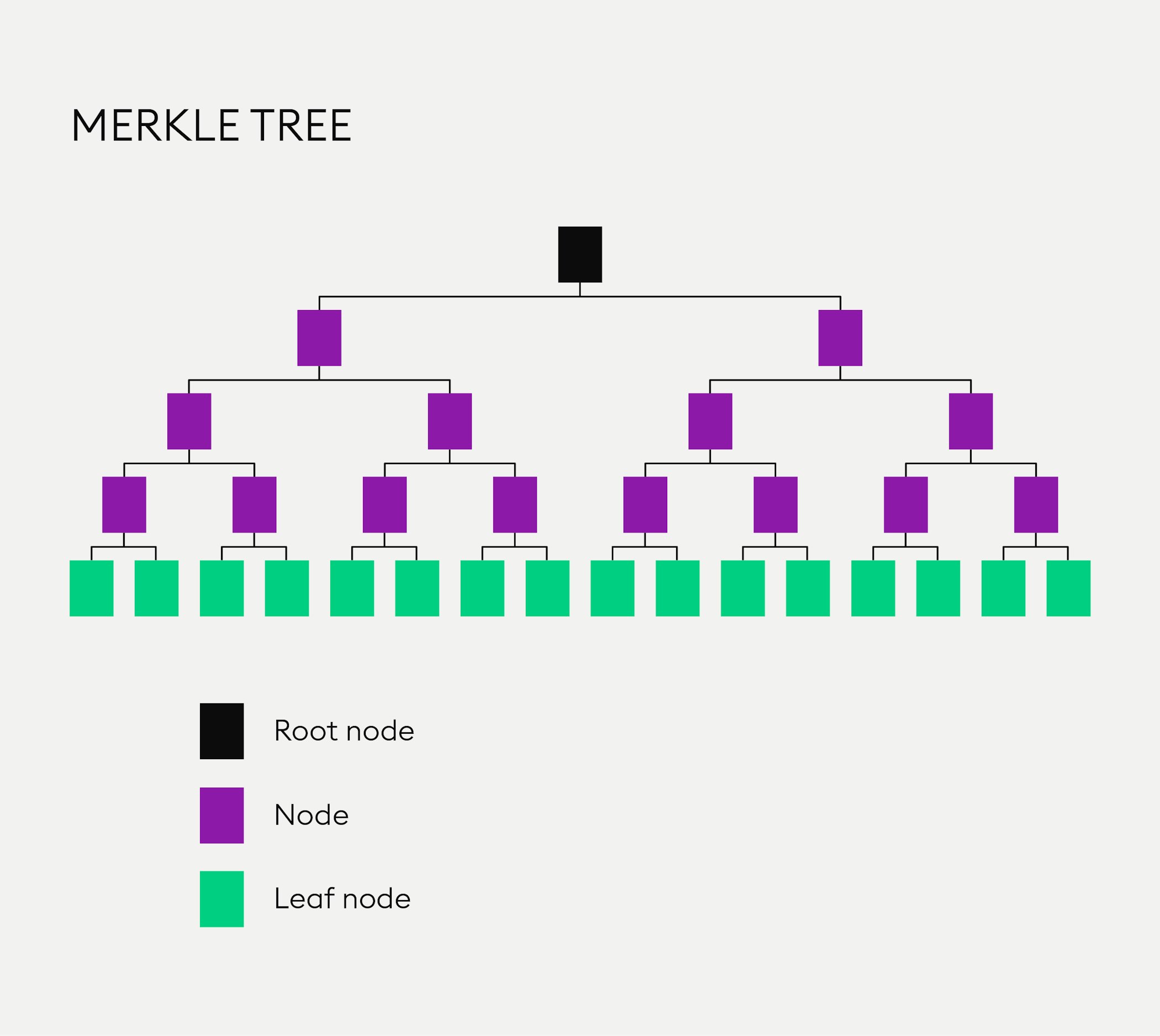
The reason for this, as you can see, is that the hash tree is a tree-like structure, with each leaf node being a hash of a block of data. Merkle trees typically use a binary-tree structure but a higher level of output can be used as well. The set-up of a perfect Merkle tree is that the number of leaves is always 2n, with the value “n” being 1, 2, 3 etc. Each node has no child node or two “child nodes”.

How are Merkle trees used in blockchain technology and why?

In the Bitcoin network, all the transactions inside a block are summarised in a Merkle tree by producing a digital fingerprint of the entire set of transactions. This way a user is able to verify whether a transaction is included in a block or not.

All nodes in the tree-like structure of the Merkle tree are partial representations of the hashed data underneath them. 

Now you may ask yourself why a hash tree is needed to prove this? Wouldn’t it be possible to hash all messages (the original data), put the hashed values into one single string and get the value of the root hash this way? Why do Merkle trees make life easier?

The issue of trust

Imagine life without Merkle trees. Instead of the Merkle root, we would store a hash of all the transactions from the blockchain in the block header. This means: in order to verify just one transaction, you would have to download the data from all of them. 

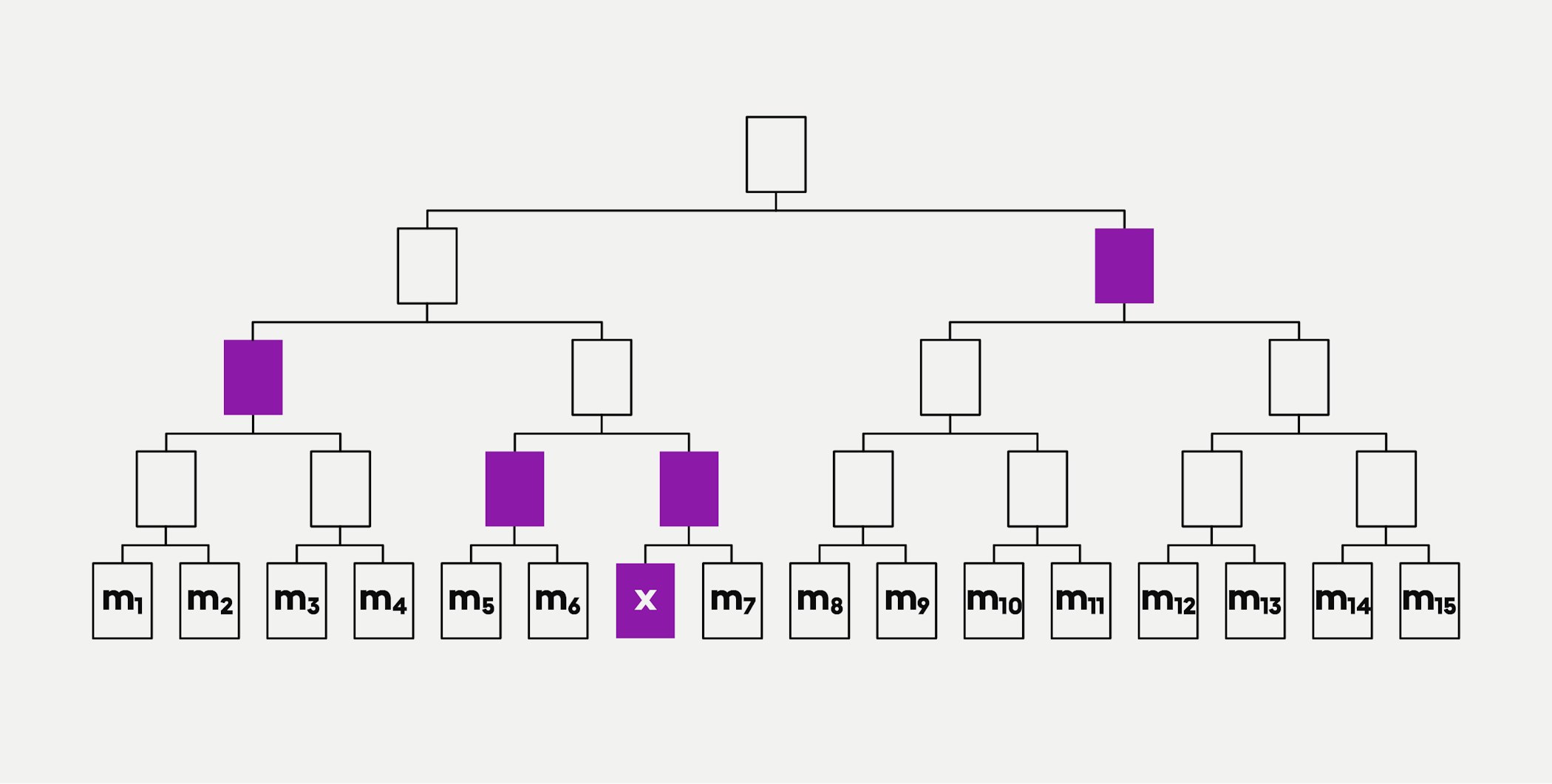
Merkle trees reduce the amount of data needed for verification. Let us say Sue wants to prove to John that the transaction “m6” has not been tampered with. John could obtain the root hash from a trusted source and verify that this is the case. 

If Sue and John proceeded without Merkle trees, Sue would need to provide John with all the hashed transactions to prove that “m6” has not been tampered with. A Merkle tree provides a much better way to verify this. Again, John gets the root from a source he trusts. This time, if Sue wants to prove that “m6” has not been tampered with, she only needs to send the message and four hashed values (shown in purple) to John as outlined in the graphic below: 

All nodes in the tree-like structure of the Merkle tree are partial representations of the hashed data underneath them. The leaves in the Merkle tree are hashes of individual transactions. 

Checking for inconsistencies

In distributed, peer-to-peer networks such as the Bitcoin blockchain, the same data exists on every computer in the peer-to-peer network. Each time the blockchain is altered through the addition of a transaction, changes are reflected simultaneously on every computer in the entire network.

John can now reconstruct that portion of the Merkle tree that is relevant to find the Merkle root. He can use this to verify the hashed values from an untrusted source. If the reconstructed root hash matches the root hash value from the trusted source, he can accept them. It is easier to recreate a portion of a Merkle tree than to verify the data against all the hashed data - and just as safe.

In summary, using a Merkle tree for checking inconsistencies considerably speeds up the validation process as only hashes and files that are not yet complete are being sent across a network, not only making the process more convenient but also using up much less memory space on a computer.